代数幾何学とは，代数学と幾何学を行き来する数学の一分野です．

初歩的な例

初歩的な具体例として，$x^3-y^2$という多項式で定まる曲線$C$を考えてみましょう． この曲線$C$はつまり，座標が$x^3-y^2=0$を満たす点$(x,y)$の集合です．

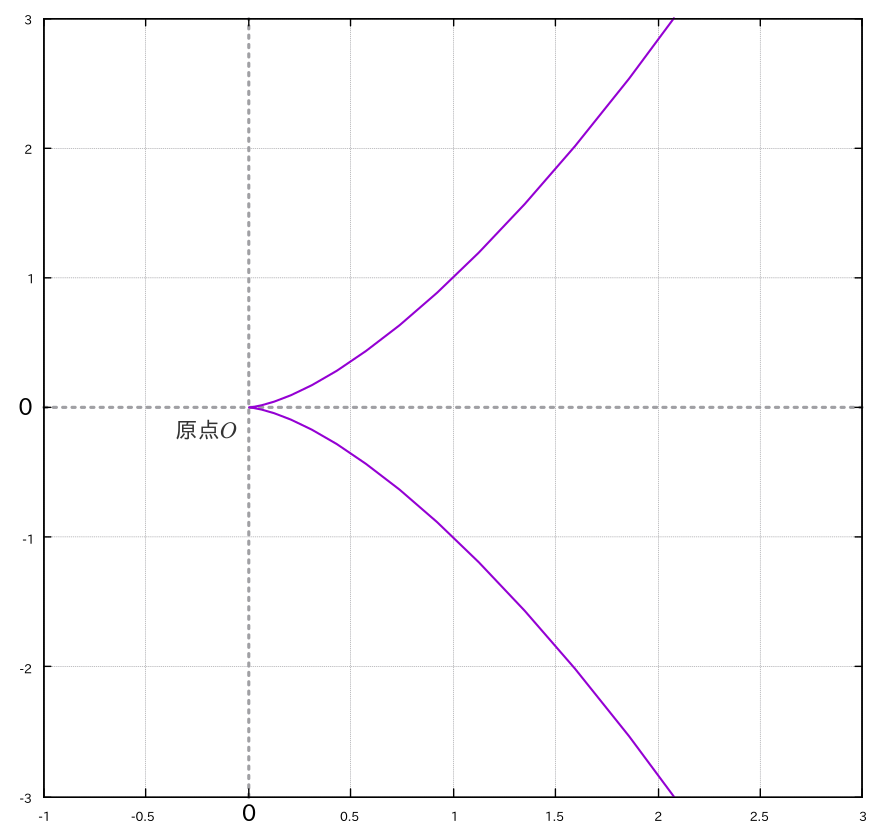
曲線$C$が$x^3-y^2$という多項式を出自に持つということを一旦忘れて， 曲線$C$をただ図形として眺めてみます． すると，一点が尖っていることに目が向きますね． このように尖っている点（この場合は原点$(0,0)$）は曲線$C$の特異点 (singular point)と呼ばれます． 厳密には特異点はこのように定義されませんが，ここはこれで良いとします．

今，図形としてみた曲線$C$が特異点を持つ事が分かりましたが， 実は曲線$C$を描かなくてもこのことが分かります． 曲線$C$が特異点を持つかどうかということは， 多項式$x^3-y^2$を代数的な操作のみを用いて調べれば分かるのです． 具体的には，これは次のような 1x2 行列の階数が， $x=0, y=0$のときに$(2-1=)1$より小さくなる（つまり階数が$0$になる）ことからわかります． \begin{bmatrix} 3x^2 & 2y \end{bmatrix}

多項式で定まる曲線に関しては， 「特異点を持つかどうか」という性質は図形を調べて分かる幾何的な性質でも有るし， 多項式だけからでも分かる代数的な性質でも有る，というわけです．

代数学と幾何学の結びつき

多項式で定まる図形はアフィン代数多様体 (affine algebraic variety) と呼ばれます． これはつまり，代数的なもの（多項式）に由来する幾何的なもの（図形）なわけです． したがってアフィン代数多様体は幾何的な側面と代数的な側面の両方を持ちます．

最初の例ではアフィン代数多様体の「特異点を持つ」という幾何的な性質が 多項式の代数的な性質として現れることを見ました． 逆に多項式の代数的な性質がアフィン代数多様体の幾何的性質として現れることもしばしば有ります． 例えば元々の多項式が二つの（定数でない）多項式の積として書ける時， 対応するアフィン代数多様体は二つの「既約成分」に分けることが出来ます．

このような現象を見ている時， 代数幾何学者はまさに「代数学と幾何学を行き来」していると言えるでしょう． これが最初に述べた「代数幾何学とは，代数学と幾何学を行き来する数学の一分野です．」という言葉の意味です．

スキームへ，更なる一般化へ

アフィン代数多様体は数学の歴史の中でも古くから扱われていました． 現代的には，スキーム (scheme)が代数幾何学の中心的研究対象です． スキームは可換環 (commutative ring) と呼ばれる純粋な代数的対象から出発して構成されます． 可換環からアフィンスキームというものが構成され，これを貼り合わせて一般のスキームが作られます． アフィン代数多様体はアフィンスキームの理想的に扱いやすい場合として扱われるように成りました．

スキームの誕生には Weil予想 というものが深く関わっています． 「この予想を解決するには（アフィン）代数多様体では手狭だ，足りない」という理由で 代数多様体が一般化されたのです． さらに「スキームでは手狭だ，足りない」というわけで代数的空間 (algebraic space)などが生まれ， 「まだ足りない」とArtin スタック (Artin stack)というものも生まれています．

スキームの一般化は他にもいっぱいあります．私が知る限りのものを列挙してみます（順番は適当です）．

• Formal schemes,
• Schemes over $\mathbb{F}_1$,
• Blue schemes,
• Rigid spaces,
• Adic spaces,
• Non-commutative schemes,
• Higher stack.

いずれも何かの問題を解決するために，あるいは興味深いために生まれ，研究されています．